题目简述
给定一个 $N\times M$ 的网格,请计算三点都在格点上的三角形共有多少个。注意三角形的三点不能共线。
思路
直接求三角形的个数比较困难。我们知道在网格中随便选三个不共线的格点就可以构成一个三角形,所以总选法减去三点共线的方案数就是三角形的个数。
横纵向三点共线的方案很好统计:对于题目中 $N$ 行 $M$ 列的网格,每行有 $M+1$ 个点,三点共线的方案数就是 $C^3_n$,因为有 $N$ 行所以横向三点共线总方案数一共是 $N \times C^3_n$;纵向可以使用相同的方法算出。
接下来我们考虑一下斜向三点共线的方案数:选定三点中的两个点作为一条线段上的两个端点,线段上(除两端点)的格点数就是在两点确定的情况下三点共线的方案数。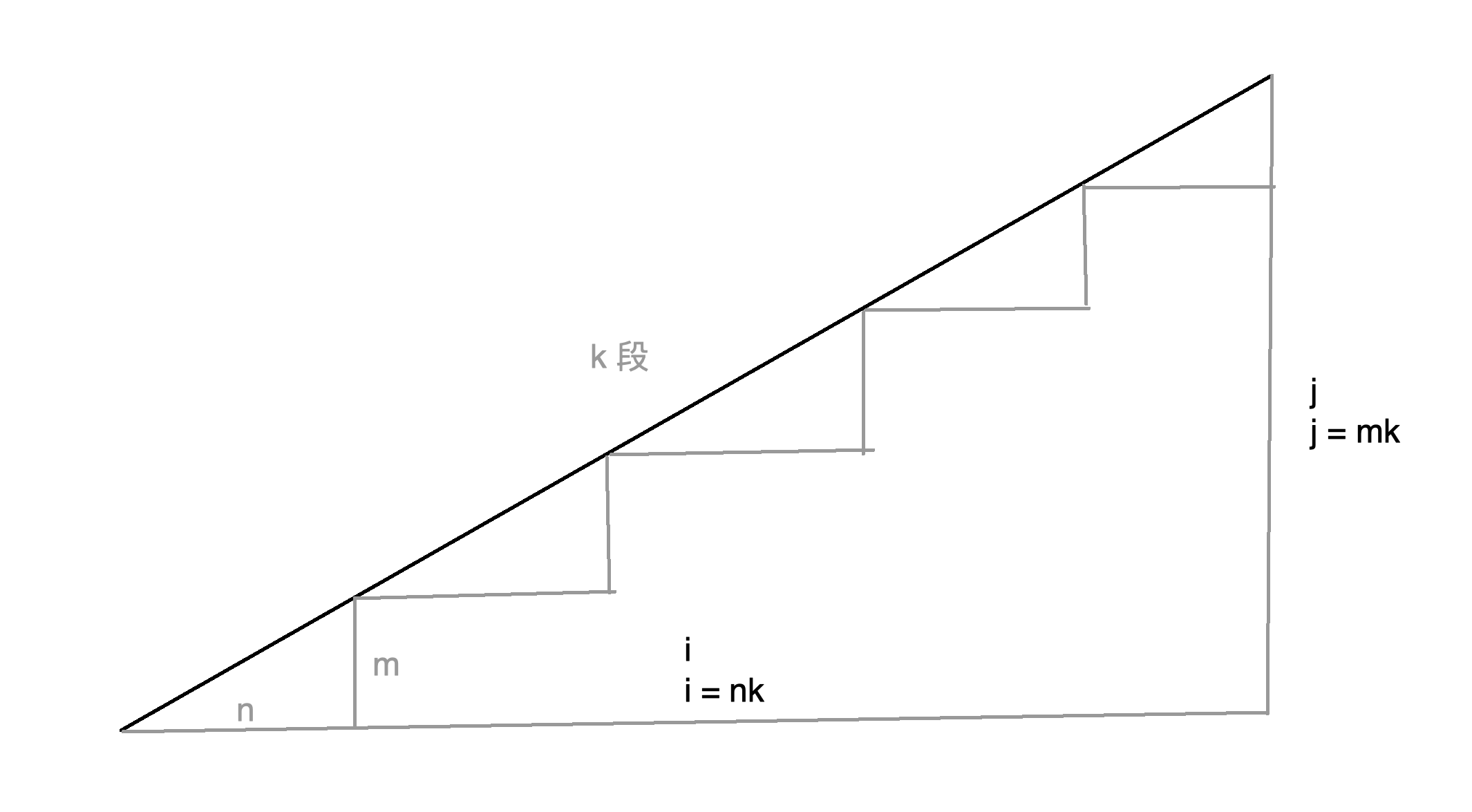 不妨看一下这张图:黑色的线是我们选定两端点构成的线段,添加灰色的辅助线我们可以以它为斜边扩展成一个两条直角边分别为 $i$,$j$ 的直角三角形。如果其中还有 $i=nk$,$j=mk$,那么我们还可以找到正好 $k$ 个小三角形,它们的两条直角边分别是 $n$,$m$,斜边是原来的线段上均等的 $k$ 段。为什么是这样呢?如果把左下的端点看作平面直角坐标系上的原点,那么右上的端点坐标就是 $(i,\ j)$。这条线段所处的直线是正比例函数 $y=kx$,其中斜率 $k=\frac{j}{i}=\frac{m}{n}$。线段上的点都满足这个关系式,但是因为是在网格图上,可选的只有坐标为整数的点。约去 $i$ 与 $j$ 的最大公约数 $k$,所得的 $m$ 和 $n$ 便是按照上面的的方法画出的小直角三角形的直角边长度。因为约去了 $k=GCD(i,j)$,所以一共有 $k$ 个这样的小三角形,即线段可以被格点分成 $k$ 段,也就是有 $k-1$ 个可选的中间点。
不妨看一下这张图:黑色的线是我们选定两端点构成的线段,添加灰色的辅助线我们可以以它为斜边扩展成一个两条直角边分别为 $i$,$j$ 的直角三角形。如果其中还有 $i=nk$,$j=mk$,那么我们还可以找到正好 $k$ 个小三角形,它们的两条直角边分别是 $n$,$m$,斜边是原来的线段上均等的 $k$ 段。为什么是这样呢?如果把左下的端点看作平面直角坐标系上的原点,那么右上的端点坐标就是 $(i,\ j)$。这条线段所处的直线是正比例函数 $y=kx$,其中斜率 $k=\frac{j}{i}=\frac{m}{n}$。线段上的点都满足这个关系式,但是因为是在网格图上,可选的只有坐标为整数的点。约去 $i$ 与 $j$ 的最大公约数 $k$,所得的 $m$ 和 $n$ 便是按照上面的的方法画出的小直角三角形的直角边长度。因为约去了 $k=GCD(i,j)$,所以一共有 $k$ 个这样的小三角形,即线段可以被格点分成 $k$ 段,也就是有 $k-1$ 个可选的中间点。
刚才只是对于一个固定的线段分析的,同样形态的线段可以在网格中的多个位置出现,线段也会有不同的形态。我们可以枚举 $i$ 和 $j$ 处理不同形态的线段,并将结果乘以它横纵可以移动的范围。当然更简单的理解方法是将线段抽象成一个向量,仍然枚举 $i$ 和 $j$ 并让它在网格中移动。
值得注意的是,$N\times M$ 的网格横纵点数都要加一,而且如果默认讨论两端点在左下和右上,实际的方案数还要乘以 2。
Code
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<climits>
#include<utility>
#define int long long
using namespace std;
int n, m, ans;
inline int GCD(int a, int b){
return b>0 ? GCD(b, a%b) : a;
}
signed main(){
scanf("%lld%lld", &n, &m);
n++, m++;
ans = (n*m)*(n*m-1)*(n*m-2)/6;
if(n >= 3) ans -= (n*(n-1)*(n-2)/6) * m;
if(m >= 3) ans -= (m*(m-1)*(m-2)/6) * n;
for(int i=1;i<n;i++)
for(int j=1;j<m;j++){
ans -= (n-i)*(m-j)*(GCD(i,j)-1)*2;
}
printf("%lld", ans);
return 0;
}