问题描述
原题写的很麻烦,简单来说就是:n 个数依次进栈,可以随机出栈,求共有几种可能
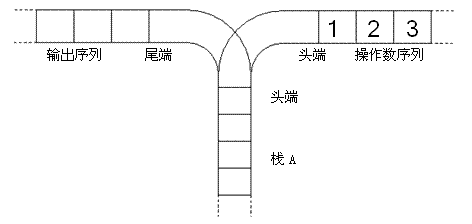
看到这道题可以想到DP,不要问为什么想不到,问就是做的题太少
既然已经明确了DP的思路,就很容易可以想到本题的阶段是已出栈数字的个数,f[i]表示有 i 个数出栈A后的方案个数,这样一来边界也很好确定,即f[0]=1,f[1]=1;
如果我们设x是到目前为止最后一个出栈A的数(则x有n种取值),则可以将已近出栈排入输出序列的数分成两部分:
- >x
- <x
操作数序列中的数由1递增至n,所以 :
<x 的数有x-1个,方案数为$f_{x-1}$
>x 的数有n-x个,方案数为$f_{n-x}$
n 确定时 x 不确定,故 x-1 和 n-x 互相影响,则一个 x 的方案数有$f_{x-1}\times f_{n-x} $
又因为 x 本身的取值有 n 种,所以有:
$Ans=f_0\times f_{n-1}+f_{1}\times f_{n-2}+…+f_{n-1}\times f_0$
f[0]=1;f[1]=1;
for(int i=2;i<=n;i++){
for(int j=0;j<i;j++){
f[i]+=f[j]*f[i-j-1];
}
}
然后就会发现,自己写出了卡特兰数的递推式:
$C_{n+1}=C_0C_n+C_1+C_{n-1}+…+C_nC_0$