题目简述
$n×m$ 的网格图,每一小格代表一个单位区域,单位区域上要么是空地,要么是导弹发射器,要么有一定数量的叛军,一个导弹发射器只能消灭一个方向的一个单位区域的叛军,求最多可以消灭多少叛军。保证不会有导弹发射器能炸到另一个导弹发射器,导弹的飞行路线不能有交叉。
$n,m≤50$
思路
先不考虑导弹路线不能交叉的限制,对于每一个导弹发射器就可以选择点权最大的那个点。由于每个区域只可能被一个横向和一个纵向的导弹打到(因为题目题面保证了「导弹发射器不能炸到导弹发射器」),那么我们可以把每一个点拆成两个点。
将一开始的答案ans设为每个导弹可以打到的最大点权之和,这个答案大概率是不合法的。将每个点的点权重新赋为一开始的答案减去这个点原来的点权,即ans-a[i][j],这样做的意义是当将导弹发射器与某个点匹配的时候,只需要在原答案的基础上减去这个点的新点权就可以了,至此我们通过转化将原问题变成一个「减去尽量小的点权并使答案合法」的问题。
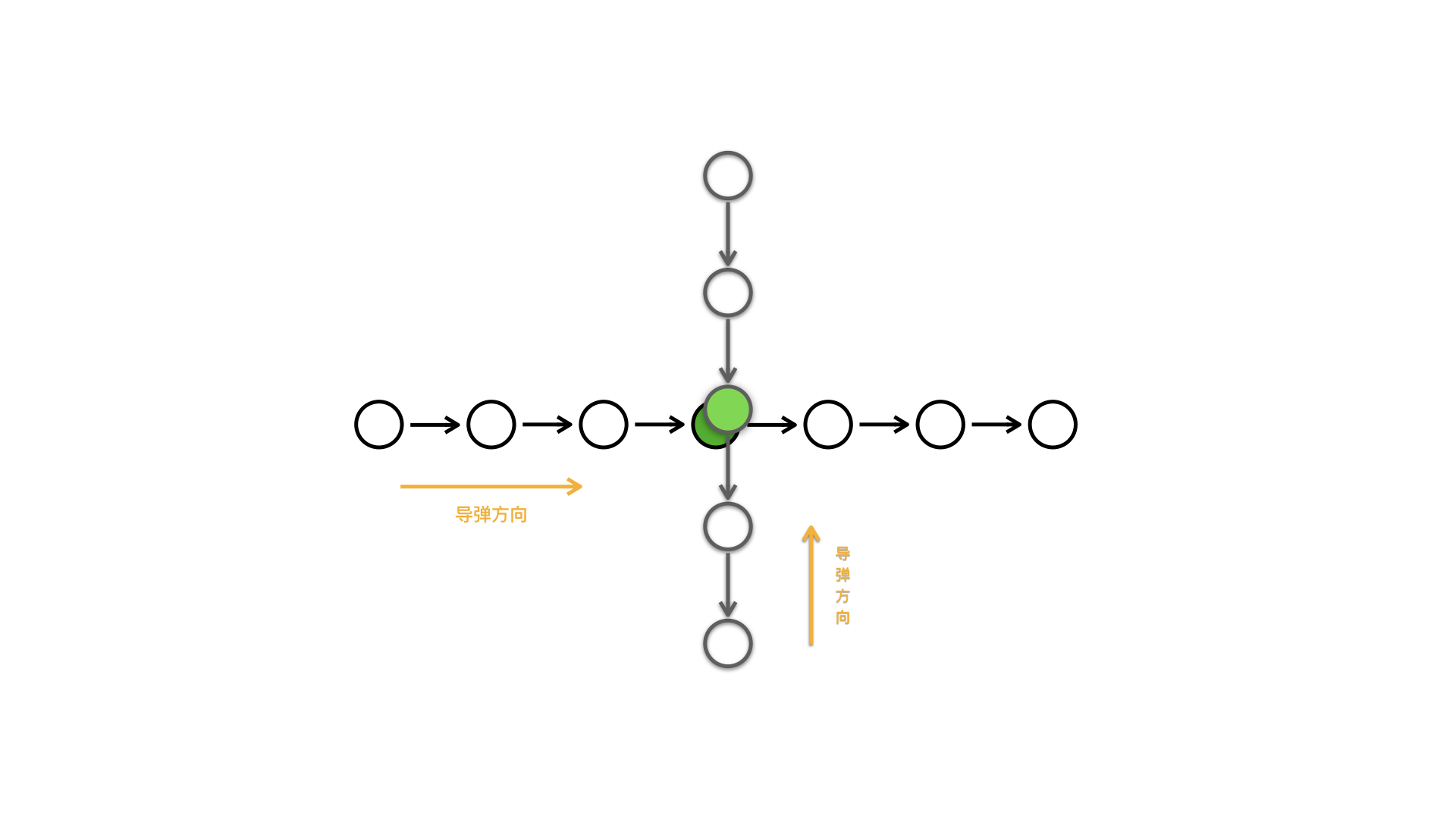
对于横点,向下一个点连一条边权为自己新点权的边,对于竖点,下一个点像自己连一条边权为自己新点权的边,可以得到上面这样的图。原来的减去一些点的点权就可以转化成删掉一些边。
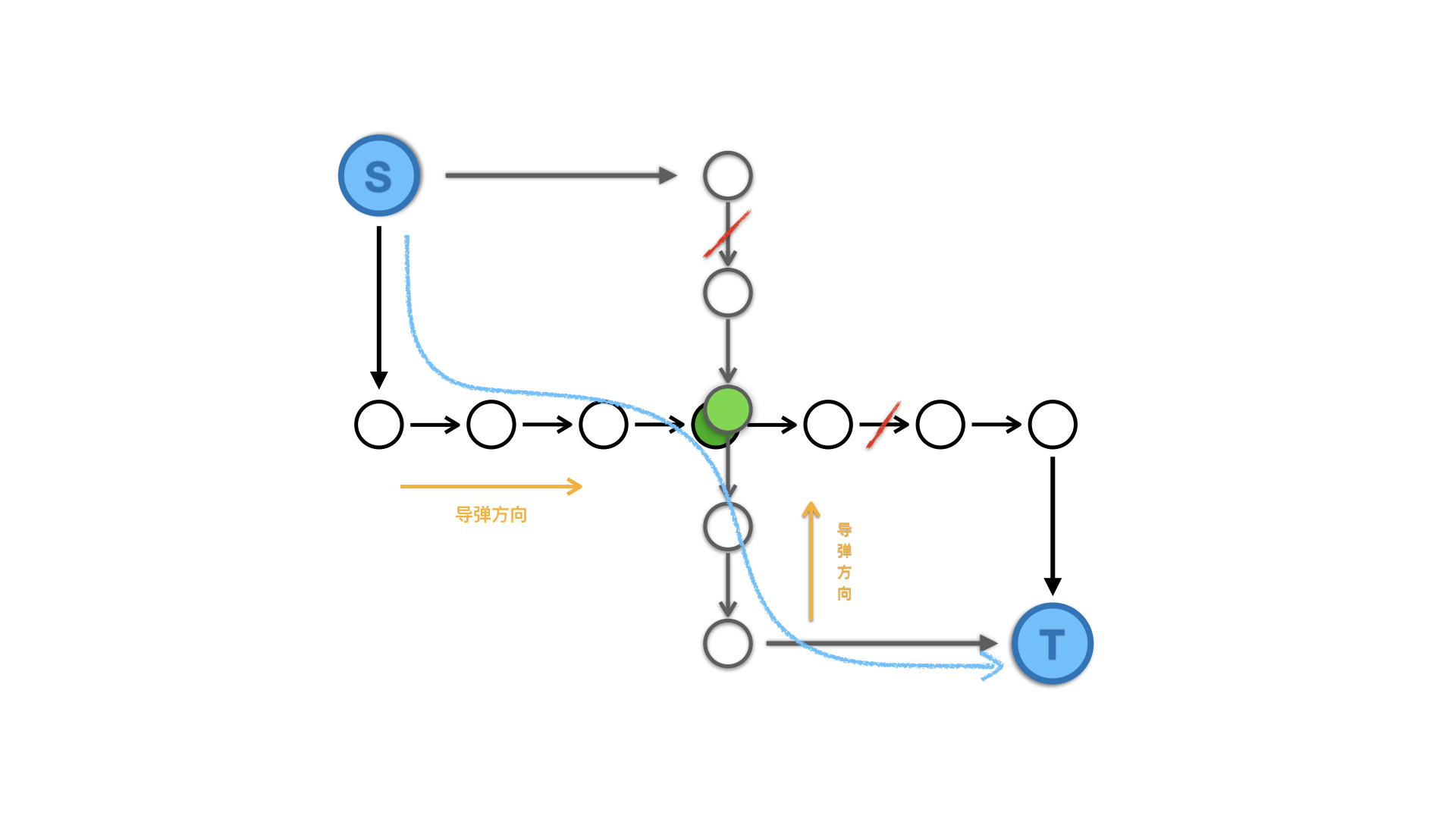
按照上图建立超级源点和超级汇点可以发现,当网络图中存在一条通路时,两发导弹的路线会相交,此时的删边时不合法的。例如上面的删边方式代表的是两发导弹分别选择了两条边到达的点,这样它们的路线会相交,此时网络图中也确实存在一条通路(蓝色)。 最终这个问题变成了要删掉边权和尽量小的边并使图中不存在通路,也就是求最小割。
至于为什么横竖的边方向不同?还记得我们一开始将一个点拆成了一个横点和一个竖点吗?这样连边可以时同一个点的横点和竖点形成通路,可以避免两个导弹同时选择这个点的情况,同时也避免了相交。
Code
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<climits>
#define int long long
#define ID1(x,y) (((x-1)*m+y)*2)
#define ID2(x,y) (((x-1)*m+y)*2-1)
using namespace std;
int n, m, ans, a[55][55], head[55*55*2], cntEdge=1, dis[55*55*2];
bool visited[55*55*2];
struct Edge{
int destination, nextEdge, value;
}edge[55*55*4*2];
inline int Read(){
int num = 0, op = 1;
char ch = getchar();
while(!isdigit(ch)){
if(ch == '-') op = -1;
ch = getchar();
}
while(isdigit(ch)){
num = num * 10 + ch - '0';
ch = getchar();
}
return op * num;
}
inline void AddEdge(int u, int v, int w){
cntEdge++;
edge[cntEdge].destination = v;
edge[cntEdge].nextEdge = head[u];
edge[cntEdge].value = w;
head[u] = cntEdge;
return;
}
inline void Link(int u, int v, int w){
AddEdge(u, v, w);
AddEdge(v, u, 0);
return;
}
inline bool Check(){
int res = INT_MAX;
for(int i=0; i<=n*m*2+1; i++){
if(visited[i]){
for(int j = head[i]; j; j = edge[j].nextEdge){
int to = edge[j].destination, val = edge[j].value;
if(val && !visited[to]){
res = min(res, dis[to]+1-dis[i]);
}
}
}
}
// printf("%lld\n", res);
if(res == INT_MAX) return false;
for(int i=0; i<=n*m*2+1; i++){
if(visited[i]) dis[i] += res;
}
return true;
}
inline int Update(int x, int y, int z){
visited[x] = true;
// printf("%lld\n", z);
if(x == y){
ans -= z;
return z;
}
for(int i = head[x]; i; i = edge[i].nextEdge){
int &to = edge[i].destination, &val = edge[i].value;
if(!visited[to] && val && dis[x] == dis[to] + 1){
int res = Update(to, y, min(z,val));
if(res){
edge[i].value -= res;
edge[i^1].value += res;
return res;
}
}
}
return 0;
}
signed main(){
n = Read(), m = Read();
for(int i=1; i<=n; i++){
for(int j=1; j<=m; j++){
a[i][j] = Read();
Link(ID1(i,j), ID2(i,j), INT_MAX);
}
}
for(int i=1; i<=n; i++){
for(int j=1; j<=m; j++){
int mx = 0;
switch(a[i][j]){
case -1:{
Link(0, ID1(i,j), INT_MAX);
for(int k=i; k>=1; k--)
mx = max(mx, a[k][j]);
for(int k=i; k>=2; k--)
Link(ID1(k,j), ID1(k-1,j), mx-max(a[k][j],0ll));
break;
}
case -2:{
Link(0, ID1(i,j), INT_MAX);
for(int k=i; k<=n; k++)
mx = max(mx, a[k][j]);
for(int k=i; k<n; k++)
Link(ID1(k,j), ID1(k+1,j), mx-max(a[k][j],0ll));
break;
}
case -3:{
Link(ID2(i,j), n*m*2+1, INT_MAX);
for(int k=j; k>=1; k--)
mx = max(mx, a[i][k]);
for(int k=j; k>=2; k--)
Link(ID2(i,k-1), ID2(i,k), mx-max(a[i][k],0ll));
break;
}
case -4:{
Link(ID2(i,j), n*m*2+1, INT_MAX);
for(int k=j; k<=m; k++)
mx = max(mx, a[i][k]);
for(int k=j; k<m; k++)
Link(ID2(i,k+1), ID2(i,k), mx-max(a[i][k],0ll));
break;
}
}
ans += mx;
Link(ID1(i,j), ID2(i,j), INT_MAX);
}
}
do{
memset(visited, false, sizeof(visited));
// printf("O");
while(Update(0, n*m*2+1, INT_MAX)){
// printf("h");
for(int i=0; i<=n*m*2+1; i++)
visited[i] = false;
}
// printf("\n");
// printf("%lld\n", ans);
}while(Check());
printf("%lld", ans);
return 0;
}